INTRODUÇÃO A FUNÇÕES

 Introdução a função


  • Uma função é uma relação matemática estabelecida entre duas variáveis.

Produto Cartesiano:

  •  Um par ordenado é formado pelos valores de x e y agrupados, os quais de terminam pontos no plano cartesiano.
  •  A coordenada (x, y) indica que os valores de x estão atribuídos à abscissa (eixo x) e os valores de y à ordenada (eixo y).
  •  Produto cartesiano é a multiplicação entre pares ordenados envolvendo conjuntos distintos.

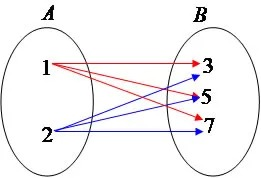
Domínio, imagem e contradomínio:

  •  Na figura abaixo há dois conjuntos numéricos, um domínio e um contradomínio.
  •  Dentro do contradomínio há um subconjunto chamado de imagem. Esse subconjunto é composto pelos elementos que estão recebendo a seta, isto é, aqueles que possuem alguma relação com os elementos do domínio.


Gráfico de uma função 

  •  É a imagem que essa função possui. Através do gráfico, podemos identificar qual é o tipo da função.

  •  A construção de gráficos é de extrema importância. Podemos dizer que assim como vemos nossa imagem refletida no espelho.
  • O gráfico de uma função é o seu reflexo.
  •  Através do gráfico, podemos definir de que tipo é a função mesmo sem saber qual é a sua lei de formação.


Plano Cartesiano → é o ambiente onde o gráfico será construído. Ele é estabelecido pelo encontro dos eixos cartesianos x e y, conhecidos como eixo das abcissas e eixo das ordenadas, respectivamente.
  • Cada ponto do gráfico é conhecido como par ordenado, pois ele é formado pelo encontro de um valor das abcissas com um valor das ordenadas.
  •  A linha que une os pares ordenados é conhecida como curva da função.




Como montar um gráfico?



1°) Escolher valores para x

Para iniciar a construção do gráfico, é necessário escolher valores para a variável x. Esses valores serão substituídos na lei de formação da função para que o valor  correspondente de y seja determinado, bem como o par ordenado. Para montar o gráfico de uma função do 1° grau, é necessário encontrar apenas dois pontos que já visualizamos no gráfico.


É também importante escolher valores próximos, como números subsequentes. Além disso, é sempre bom saber os pontos em que x = 0 e y = 0 (zero da função).

Considere a função y = x + 1.
     Segue uma tabela com os valores de x para encontrar os valores de y:


2) Encontrar os pares ordenados no plano cartesiano

Lançando cada um desses pares ordenados no plano cartesiano, encontramos os seguintes pontos:



  










Comentários

Postar um comentário

Postagens mais visitadas deste blog

FUNÇÃO AFIM

Imagem
 FUNÇÃO AFIM  Também chamada de função do 1º grau, é uma função f : ℝ→ℝ  Definida como  f(x) = ax + b , sendo  a  e  b  números reais.   O número  a  é chamado de coeficiente de x e representa a taxa de crescimento ou taxa de variação da função. Já o número  b  é chamado de termo constante.  Polinomial  do  1º grau/ indentidade  É a mais simples;  F:R→R (reais em reais)  A função identidade, onde  y = f(x) = x.    Sua fórmula: y = f(x) = ax + b Os valores do seu domínio são os mesmos da imagem do contradomínio. Gráfico de uma Função do 1º grau O gráfico de uma função polinomial do  1º grau  é uma reta oblíqua aos eixos  Ox  e  Oy .   Para construirmos seu gráfico basta encontrarmos pontos que satisfaçam a função. Exemplo 1: Construa o gráfico da função f (x) = 2x + 3. Solução: Para construir o gráfico desta função, vamos atribuir valores arbitrários para x, substituir na equação e calcular o valor correspondente para a f (x). Sendo assim, iremos calcular a função para os valores de x i
Leia mais